Alex Verdugo Revisited: A Deeper Dive into His MLB Stats and Career Progression

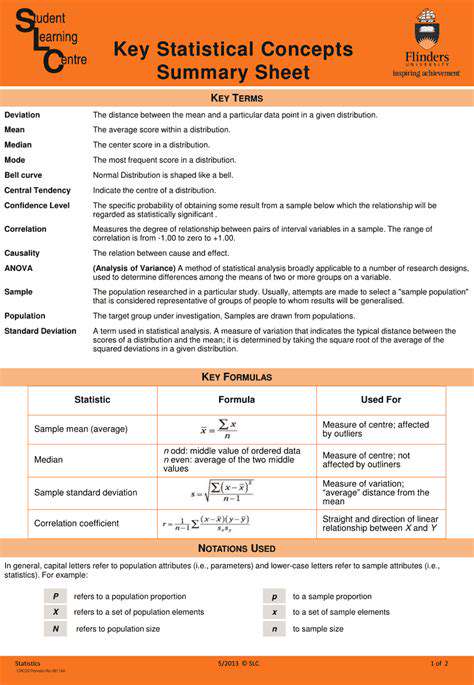
Understanding the Basics of Statistical Analysis

Statistical analysis is a crucial tool in various fields, from scientific research to business decision-making. It involves collecting, organizing, analyzing, interpreting, and presenting data to draw meaningful conclusions. This process relies on a range of methods, including descriptive statistics to summarize data and inferential statistics to make predictions about a larger population based on a sample. Understanding the fundamental principles of statistical analysis is essential for interpreting research findings accurately and making informed decisions. By applying these methods, we can gain valuable insights and identify patterns that might otherwise remain hidden within the data.

Different statistical techniques are employed depending on the nature of the data and the research question. For example, comparing the average heights of men and women requires different methods than analyzing the relationship between advertising spending and sales figures. Understanding these differences is key to choosing the appropriate analytical approach and drawing valid conclusions.

Comparing Datasets: Key Considerations

Comparing datasets is a common task in statistical analysis, often involving the evaluation of differences between groups or the identification of trends over time. Crucially, this comparison must be conducted with careful consideration of the variables being compared and the potential for confounding factors. For example, comparing the average income of two different cities might reveal a significant difference, but this difference could be influenced by other factors, like the cost of living or the job market. Careful consideration of these factors is paramount when interpreting the results of any comparison. Proper statistical methods should be chosen to account for potential biases and ensure that the conclusion is valid.

Different types of comparisons require different statistical tests. For instance, comparing means across multiple groups might involve ANOVA, while assessing the relationship between two variables could necessitate a correlation analysis. This section will explore different statistical tests and help readers understand their applicability in various situations.

Interpreting Results and Drawing Conclusions

Once the statistical analysis is complete, the results must be interpreted and conclusions drawn. This process involves understanding the statistical significance of findings and considering the practical implications of the conclusions. For example, a statistically significant difference in test scores between two groups might not always have practical implications in the real world. Careful consideration of the context and the potential limitations of the analysis is vital. A thorough understanding of the assumptions underlying the statistical methods used is essential for drawing accurate conclusions. Moreover, the context in which the data was gathered and the nature of the variables being studied must be taken into account when interpreting the results.

Presenting the results clearly and concisely is also crucial. This includes using appropriate graphs, charts, and tables to illustrate the findings and creating a narrative that explains the meaning behind the numbers. Effective communication of the results is essential for ensuring that the conclusions are understood and appreciated by the intended audience.